TEMA 11: DISPLAY DE 7
SEGMENTOS, CIRCUITO MANEJADOR DE DISPLAY
El
“display de 7 segmentos” es un dispositivo usado
para presentar información de forma visual. Esta información
es específicamente un dígito decimal del 0 (cero) al 9
(nueve), por lo que se intuye que que el código BCD está
involucrado. El caso que nos atañe consta de 7 LED's (Light
Emisor Diode), uno por cada segmento, que se encenderán o
apagarán dependiendo de la información que se les envíe
(dije que en este caso ya que existen también display 7
segmentos de cristal líquido, incandescentes, etc.).
El
display 7 segmentos tiene una estructura similar a:
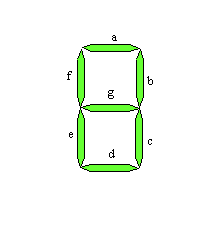
donde
los 7 led's vienen indicados por las letras a, b, c, d, e, f y g. Con
éstos pueden formarse todos los dígitos decimales. Por
ejemplo, para formar el número tres deben activarse los led's
a, b, c, d y g y desactivar los e y f. Para el uno se usan los led's
b y c (ojo, esta es la combinación correcta no e y f). De
forma análoga se procede para el resto de los casos. Veamos
como queda:
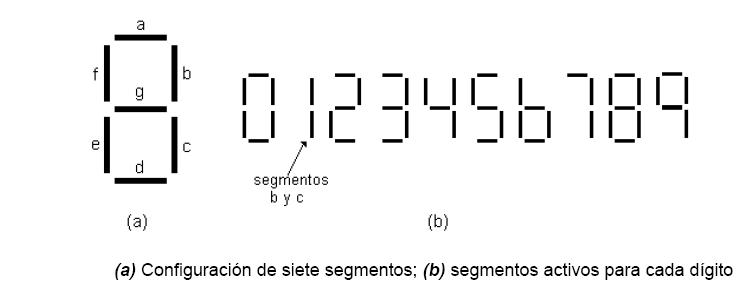
Estos
dispositivos pueden ser de tipo “Ánodo Común”
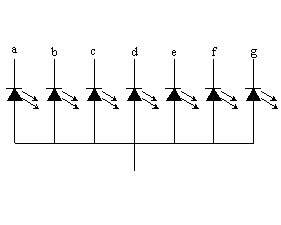
o “Cátodo Común”
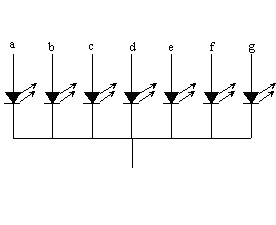
En
el caso de los display de ánodo común todos los ánodos
(+) de los led's comparten la conexión. Estos display
requieren un cero (una tierra) a la entrada de cada segmento para
encenderlo. En el caso de los display de cátodo común
todos los cátodos (-) de los led's comparten la conexión.
Estos display requieren un uno (Vcc) a la entrada de cada segmento
para encenderse. Todas las conexiones deben ser hechas a través
de una resistencia para regular la cantidad de corriente que pasa a
través de los led's.
Existen
casos donde aparece un octavo segmento que suele usarse como punto
decimal (ver el DP):
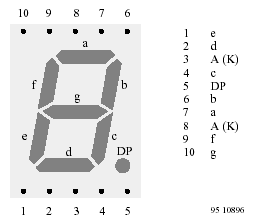
En
la figura pueden verse también una de las configuraciones de
pines más popular que contienen los display 7 segmentos y lo
que representan. Los pines 3 y 8 son el ánodo común ó
el cátodo común (dependiendo de cual sea el caso del 7
segmentos elegido) y aunque regularmente es indiferente cual de ellos
conecten existen casos de modelos de displays en los que, por sus
especificaciones, se requieren ambos conectados (o también
quizá porque requieran cumplir alguna condición de
manejo de corriente en su circuito). El encapsulado de este mismo
display luce algo como:
para
la versión que contiene sólo un dígito pero
existen algunas para más dígitos como por ejemplo el de
dos dígitos que es bastante usado o los de X dígitos y
medio donde el medio viene dado por el hecho de que él sólo
puede representar el número uno (tiene únicamente dos
segmentos).
Existen
circuitos integrados a nivel MSI que pueden realizar la tarea de
manejar estos displays. Estos IC's son decodificadores,
específicamente los conocidos como decodificadores de BCD a 7
segmentos, como son los casos de los IC 7446, 7447 y 7448 de la
familia TTL. El 7446 y 7447 tienen salidas con lógica negativa
por lo que enviarán un cero al segmento que se desea encender.
Esto quiere decir que manejan Displays 7 segmentos de ánodo
común. Ambos son Open Collector (bueno para el manejo de
corriente necesario en algunos casos) y se diferencian únicamente
en la salida que pueden manejar (30v para el 7446 y 15v para el
7447). Nuestros circuitos generalmente estarán construidos con
tecnología TTL a 5V y por ello lo más seguro es que
empleemos el 7447. En el caso del 7448 las salidas son de lógica
positiva por lo que son usados con los dispositivos cátodo
común. Todos comparten una característica: esperan a la
entrada un número en BCD y es para cada una de ellas que
desplegarán el dígito decimal correspondiente. Pero aún
así, estos IC tienen respuestas para otras combinaciones a la
entrada distintas de BCD. En el siguiente dibujo se muestran las
salidas reflejadas en los display de 7 segmentos para todas las
combinaciones binarias de 4 bits posibles:
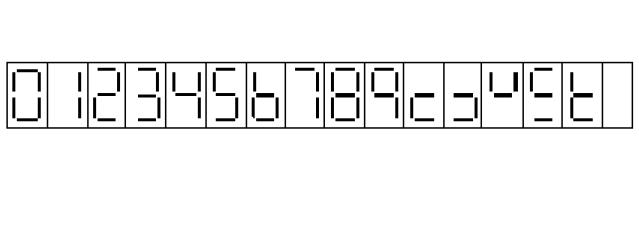
Aparte
de los dígitos decimales, se ven las salidas para cuando el
decodificador tiene entrada de 1010, 1011, 1100, 1101, 1110 y 1111.
Este último caso apaga todos los segmentos y por ello no se ve
nada.
A
continuación se muestra una implementación típica
usada para la prueba de los dislay de 7 segmentos:
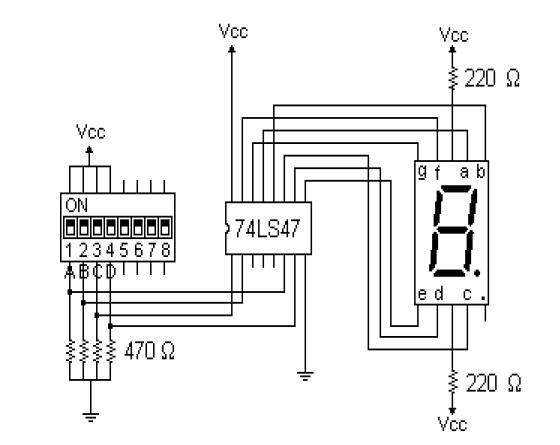
El
display mostrará el dígito decimal que corresponda con
el número binario seleccionado por los interruptores 1, 2, 3 y
4 del dip switch. En esta configuración se ve que las
resistencias delimitadoras de corriente se colocan en el ánodo
común (sabemos que son ánodo común por el uso
del 7447) pero dependiendo de la implementación, e incluso a
veces del display, en algunos casos pueden requerirse el uso de una
resistencia por cada segmento y la conexión directa de los
ánodos a Vcc.
A
continuación veremos la implementación de un circuito
decodificador de BCD a 7 segmentos usando tecnología SSI.
Hallaremos sólo las funciones y no haremos el esquemático
debido a lo grande del mismo. Asumiremos que la entada será
única y exclusivamente un número BCD válido por
lo que el resto de los casos no nos interesan (dont care). Asumiremos
también que nuestro circuito será destinado a un
display de cátodo común (por lo que tendrá
salida con lógica positiva). Para ello empecemos con la tabla
de la verdad. Sabiendo que la entrada será I (formada por
I3I2I1I0) y las salidas
serán los siete segmentos posibles a, b, c, d, e, f y g (como
ya se ha mostrado), tenemos que:
|
I3
|
I2
|
I1
|
I0
|
a
|
b
|
c
|
d
|
e
|
f
|
g
|
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
|
1
|
0
|
1
|
0
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
|
1
|
0
|
1
|
1
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
|
1
|
1
|
0
|
0
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
|
1
|
1
|
0
|
1
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
|
1
|
1
|
1
|
0
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
|
1
|
1
|
1
|
1
|
X
|
X
|
X
|
X
|
X
|
X
|
X
|
Ahora
bien. En este caso tenemos 7 funciones de salida que llamaremos a(I),
b(I), c(I), d(I), e(I), f(I) y g(I). Éstas vienen dadas por:
a(I)=∑(0,2,3,5,7,8,9)+d(10,11,12,13,14,15)
b(I)=∑(0,1,2,3,4,7,8,9)+d(10,11,12,13,14,15)
c(I)=∑(0,1,3,4,5,6,7,8,9)+d(10,11,12,13,14,15)
d(I)=∑(0,2,3,5,6,8)+d(10,11,12,13,14,15)
e(I)=∑(0,2,6,8)+d(10,11,12,13,14,15)
f(I)=∑(0,4,5,6,8,9)+d(10,11,12,13,14,15)
g(I)=∑(2,3,4,5,6,8,9)+d(10,11,12,13,14,15)
que
luego de hacer las respectivas simplificaciones por mapas de Karnaugh
nos queda:
a
= I3 + I2I0 + I2'I0'
+ I2'I1
b
= I1I0 + I1'I0' + I2'
c
= I0 + I2 + I1'
d
= I1I0' + I2'I1 + I2I1'I0
+ I2'I0'
e
= I1I0' + I2'I0'
f
= I3 + I2I0' + I2 I1'
+ I1'I0'
g
= I3 + I2 I1' + I2I0'
+ I2'I1
Partiendo
de estas funciones simplificadas se realiza la implementación.
Como
ejercicio implemente el circuito anterior con un decodificador de
salida con lógica negativa y con compuertas AND ó NAND.
Dibuje el esquemático.
También
como ejercicio haga la implementación con tecnología
SSI para cuando la salida es con lógica negativa.
En
la próxima clase se verá el TEMA 12: Comparador
de magnitud a nivel SSI y MSI.

