-
A
B
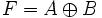
0
0
0
0
1
1
1
0
1
1
1
0
CÓDIGOS BINARIOS
Como ya vimos, los sistemas digitales usan señales eléctricas para representar dos posibles valores o estados que asociamos con cierto o falso. Como ya vimos también, para expresar información en estos sistemas hacemos uso de los números binarios ya que con ellos podemos representar los dos estados estables de los sistemas digitales a través del 0 y el 1 (y que podemos usar una combinación de éstos para representar cualquier cantidad). Muy bien, pero los sistemas digitales electrónicos pueden ser usados para procesar información discreta de cualquier tipo ya sean números decimales, letras, colores, etc y es por ésto que en la mayoría de los casos se hace conveniente el expresar la información que se desea procesar de una forma que sea más manejable. Es aquí donde entran los códigos binarios.
Como les dije en el tema pasado, al elemento mínimo de un número binario se le conoce como bit. Un bit no es más que un código binario que sólo puede representar los dos estados estables. Un bit es por definición un dígito binario.
Si se quieren expresar un número de elementos de 2n se requerirán entonces n bits para expresar dicho número de elementos. Por ejemplo si se quieren representar 4 posibilidades se requerirán entonces 2 bits ya que 22 = 4 (y de hecho estas combinaciones son 00 01 10 y 11 que, fácilmente verificable, representan los números decimales del 0 al 3). Si se quieren representar 8 elementos entonces se requieren 3 bits ya que 23 = 8 (000, 001, 010, 011, 100, 101, 110 y 111, en decimal del 0 al 7). En resumen, con n bits se pueden representar 2n opciones que irán desde 0 hasta 2n – 1.
Ahora bien, no siempre se requerirá expresar una cantidad exacta de una potencia de 2. Por ejemplo si queremos mostrar las posibilidades en los dígitos decimales requeriremos de 10 combinaciones. Por supuesto, tendremos que usar cuatro bits ya que con tres sólo podremos representar 8 de ellas. Con los cuatro bits tenemos un exceso pero lo que se hace es ignorar el resto de las combinaciones.
COMENTARIO: Debido a que he recibido esta pregunta les comento de una vez que 1kb (un kilobit) es igual a 1024 bits. Cuando hablamos en términos de números binarios, hablamos de potencias de 2. Así que 1kb = (10000000000)2 bits = 210 bits = 1024 bits. De forma análoga para 1 Kbyte (1 byte = 8 bits). Otro caso es 1 MB (un megabyte) = (100000000000000000000)2 = 220 bytes = 1048576 bytes.
CÓDIGOS DECIMALES
Entre los códigos binarios tenemos algunos que se usan para representar dígitos decimales. Las formas para representar los números decimales con códigos binarios es muy variada y depende de la lógica que se use. El más usado de todos estos códigos es el BCD (por sus siglas en inglés de “Binary Coded Decimal” o “decimal codificado en binario”). En este caso se usa una relación directa para expresar los dígitos decimales. ¿Qué quiero decir con directa? Pues bien, que al convertir el número binario a decimal obtendrás el dígito decimal en cuestión. Por ejemplo para expresar el (0)10 usamos 0000, para el (5)10 0101 y para el (9)10 1001 (más adelante mostraré una tabla con todas las combinaciones). La forma de calcular el número binario para representar el dígito decimal viene dada por la fórmula explicada en el tema anterior pero para realizar un cálculo rápido recuerden que la carga del primer dígito binario representa 8, la del segundo 4, la del tercero 2 y la del cuarto y último representa 1. Por supuesto que en BCD no existen 1100, 1010, etc ya que éstas no muestran ningún dígito decimal. Otro ejemplo: para representar el dígito decimal 6 en código BCD sería: 0110 ya que:
0 x 8 + 1 x 4 + 1 x 2 + 0 x 1 = 6
Un código decimal que se ha usado en algunos computadores viejos es el código de “exceso a 3”. Este último es un código sin carga, cuya asignación se obtiene del correspondiente valor en BCD una vez se haya sumado 3. Ejemplo (0)10 = 0011, (9)10 = 1100, etc.
También es posible asignar cargas negativas a un código decimal, como por ejemplo en el código 8, 4, -2, -1. En este caso la combinación de bits 0110 se interpreta como el dígito decimal 2, ya que como se ve:
0 x 8 + 1 x 4 + 1 x (-2) + 0 x (-1)=2
Del libro “Lógica digital y diseño de computadores” de M. Morris Mano: “Los números se representan en computadores digitales en binario o decimal a través de un código binario. Cuando se estén especificando los datos, el usuario gusta dar los datos en forma decimal. Las maneras decimales recibidas se almacenan internamente en el computador por medio del código decimal. Cada dígito decimal requiere por lo menos cuatro elementos de almacenamiento binario. Los números decimales se convierten a binarios cuando las operaciones aritméticas se hacen internamente con números representados en binario. Es posible también realizar operaciones aritméticas directamente en decimal con todos los números ya dejados en forma codificada. Por ejemplo, el número decimal 395, cuando se convierte a binario es igual a 110001011 y consiste en nueve dígitos binarios. El mismo número representado alternamente en código BCD, ocupa cuatro bits para cada dígito decimal para un total de 12 bits: 001110010101” ... esto último por 0011 1001 0101.
OJO: No es lo mismo convertir un número decimal a binario que convertir un número decimal a codificación binario. Por supuesto en ambos casos obtendremos un número en binario, pero no el mismo. Ojo con eso.
El código BCD es el más común a la hora de trabajar dígitos decimales en código binario, pero los otros casos que comenté: exceso a 3 y 8 4 -2 -1 tienen una peculiaridad muy interesante y es que estos números son autocomplementarios. Esto quiere decir que el complemento a 9 del número decimal se obtiene con tan sólo intercambiar el estado de los bits del código binario. Por ejemplo, el número cero tiene un código binario en “exceso a 3” de 0011. Si intercambiamos los estados de los bits obtenemos 1100 que es la representación en exceso a 3 del número decimal 9 que es a su vez el complemento a 9 de cero. Se observa que ésto puede ser muy útil a la hora de realizar operaciones aritméticas internas de números decimales en código binario en particular en el caso de la resta que puede realizarse por complemento a 9.
A continuación veamos una tabla que resume los modos de presentar información en binario en los distintos ”códigos decimales” vistos
|
DÍGITO DECIMAL |
BCD |
EXCESO A 3 |
84-2-1 |
|
0 |
0000 |
0011 |
0000 |
|
1 |
0001 |
0100 |
0111 |
|
2 |
0010 |
0101 |
0110 |
|
3 |
0011 |
0110 |
0101 |
|
4 |
0100 |
0111 |
0100 |
|
5 |
0101 |
1000 |
1011 |
|
6 |
0110 |
1001 |
1010 |
|
7 |
0111 |
1010 |
1001 |
|
8 |
1000 |
1011 |
1000 |
|
9 |
1001 |
1100 |
1111 |
Algunos códigos binarios presentan propiedades de detección de error y de ellos hablaremos a continuación.
CÓDIGOS DE DETECCIÓN DE ERROR
Los sistemas digitales procesan información binaria haciendo uso de señales. Por supuesto que ellas deberán ser transmitidas de alguna forma entre los distintos componentes del sistema para poder así transferir la información. Ésto se hace a través de un medio de comunicación. En nuestro caso particular que usamos señales eléctricas, la transmisión se realiza, por ejemplo, a través de cables de cobre pero también puede ser hecha por ondas de radio, fibra óptica, etc dependiendo del tipo y del medio en el que deben transmitirse las señales. Es por ésto que se hace necesario contar con una forma de detección de errores. De no tenerlo, cualquier “ruido” que se produzca en el transporte podría alterar el dato que está siendo transmitido y por ende no podríamos tener la certeza de que la información que estamos recibiendo sea la correcta. Ésto puede no ser importante en algunos casos como por ejemplo en las transmisiones de radio o televisión pero en cambio es vital en un sistema digital. Imagínense en el más sencillo caso: una calculadora a la que introduzcamos dos números a sumar y que no podamos confiar en el resultado que ésta arroje. Pues bien, para poder detectar un posible error pueden usarse códigos de detección de errores. El código como tal no corregiría el error pero sí indicaría su presencia. Esto entonces puede ser tomado en cuenta para tomar las medidas que sean necesarias ya sea un rediseño del sistema en el caso de que el error sea demasiado frecuente ó, en el caso que sea eventual, la inclusión de una lógica que instruya al sistema a realizar nuevamente la operación.
Uno de los métodos usados para la detección de errores es el bit de paridad. Cuando se quiere generar un código de error basado en el bit de paridad lo que se hace es agregar un bit al dato original. Supongamos que trabajamos con palabras de 4 bits. En este caso, luego de pasar el número por un generador de paridad y agregar el bit resultado a la palabra original, obtendríamos una palabra de 5 bits. La paridad puede ser tanto par como impar. En el caso de que sea paridad impar, el bit de paridad que se le agregue será aquel que haga que la nueva palabra contenga un número impar de unos. Por ejemplo, si tenemos el número: 0010, el bit a agregar para reflejar una paridad impar debe ser 0. Esto debido a que la suma de los bits que son “1” es impar. En otro caso, al número 0011, siguiendo con paridad impar, deberá ser agregado el bit 1. De esta forma el número de “1” en toda la palabra resultante será impar. El caso de paridad par es análogo sólo que aquí el bit que se agrega será para completar un número PAR de “1”. En “paridad par” el mismo ejemplo 0010 generaría el bit de paridad “1” resultando en total en un número par de unos. Éste es el caso más sencillo de bit de paridad y obviamente se nota que este tipo de método es sólo útil si el número de errores en la palabra es 1, 3, en fin, un número impar de errores. Existen formas de generar paridad más complejas que ayudarían en los otros casos pero que no serán cubiertas, al menos no por ahora. En todo caso, éste es sólo uno de los códigos de detección de errores.
CÓDIGO REFLEJADO
Tenemos también el “código reflejado” o “código gray”. Sacado de la Wikipedia (http://es.wikipedia.org/):
“El Código Gray es un caso particular de código binario. Consiste en una ordenación de 2n números binarios de tal forma que cada número sólo tenga un dígito binario distinto a su predecesor. Esta técnica de codificación se originó cuando los circuitos lógicos digitales se realizaban con válvulas de vacío y dispositivos electromecánicos. Los contadores necesitaban potencias muy elevadas a la entrada y generaban picos de ruido cuando varios bits cambiaban simultáneamente. El uso de código Gray garantizó que en cualquier transición variaría tan sólo un bit. En la actualidad, el código Gray se sigue empleando para el diseño de cualquier circuito electrónico combinacional mediante el uso de un Mapa de Karnaugh, ya que el principio de diseño de buscar transiciones más simples y rápidas entre estados sigue vigente, a pesar de que los problemas de ruido y potencia se hayan reducido.”
En el tema anterior comentamos que los sistemas digitales pueden ser usados sólo para procesar datos discretos pero que existen diversas señales que son continuas (como el sonido) y que para llevar esas señales a un medio discreto necesitaríamos de un convertidor analógico a digital. El código gray también puede ser usado en los casos que requerimos procesar la información proveniente de un medio continuo o analógico ya que el cambio que presenta dicha señal será reflejado de forma continua en el entorno digital alterando tan sólo un bit entre los estados. El cálculo del código gray de un número puede realizarse de forma sencilla haciendo una XOR del número a convertir con él mismo pero desplazado un bit hacia la derecha y descartando el bit menos significativo del resultado. La XOR es una operación lógica y ya hablaremos de ella más adelante.
A continuación les presento una tabla en la que se muestran los números binarios del 0 al (15)10 y sus respectivos bits de paridad par, paridad impar y código gray.
|
Número decimal |
Número binario |
Bit de paridad impar |
Bit de paridad par |
Código gray |
|
0 |
0000 |
1 |
0 |
0000 |
|
1 |
0001 |
0 |
1 |
0001 |
|
2 |
0010 |
0 |
1 |
0011 |
|
3 |
0011 |
1 |
0 |
0010 |
|
4 |
0100 |
0 |
1 |
0110 |
|
5 |
0101 |
1 |
0 |
0111 |
|
6 |
0110 |
1 |
0 |
0101 |
|
7 |
0111 |
0 |
1 |
0100 |
|
8 |
1000 |
0 |
1 |
1100 |
|
9 |
1001 |
1 |
0 |
1101 |
|
10 |
1010 |
1 |
0 |
1111 |
|
11 |
1011 |
0 |
1 |
1110 |
|
12 |
1100 |
1 |
0 |
1010 |
|
13 |
1101 |
0 |
1 |
1011 |
|
14 |
1110 |
0 |
1 |
1001 |
|
15 |
1111 |
1 |
0 |
1000 |
NOTA: Obsérvese que los cambios continuos en código gray son representados con el cambio de un solo bit a la vez.
CÓDIGOS ALFANUMÉRICOS
Y ¿qué pasa cuando el dato que quiero manejar es una letra? Aquí se hace necesario el expresar este elemento discreto de una forma binaria y para ello usamos algún código binario alfanumérico. Así expresamos las letras del alfabeto y algunos símbolos necesarios como la coma, el punto, etc. Yo les hablaré en particular del código ASCII (por American Standard Code for Information Interchange) que es un código de 7 bits que se usa para expresar las letras mayúsculas, minúsculas y los símbolos más usados. Este código es aún usado actualmente por las computadoras y es por ello que es éste el que menciono. Por supuesto existen otros como el código interno (de 6 bits) y el código EBCDIC (Extended BCD Interchange Code de 8 bits), sólo que el ASCII es, por así decirlo, más usado. Al ser el código ASCII un código de 7 bits, en implementaciones digitales se suele usar el 8avo bit (que completa 1 byte) como bit de paridad. En las tablas ASCII usadas en las computadoras la letra A es siempre mostrado con el número binario correspondiente al decimal 65 (100 0001), la B con el 66 (100 0010) y así sucesivamente hasta llegar a la Z con el 90 (101 1010). Los caracteres que representan símbolos, letras minúsculas y números, estos últimos empezando por el decimal 48 con el caracter 0, también tienen su sitio dentro de la tabla ASCII.
Lo importante de resaltar aquí es que la mayoría de los elementos discretos a los que estamos acostumbrados tienen una forma de ser expresados en el mundo binario a través de un Código Binario.
ÁLGEBRA DE BOOLE
El Álgebra de Boole de forma análoga a cualquier otro sistema matemático deductivo puede ser definida por un conjunto de elementos, operadores y postulados. Del libro “Lógica Digital y Diseño de Computadores” de M. Morris Mano: “Un conjunto de elementos es una colección de objetos que tienen una propiedad común. Si 'S' es un conjunto y 'x' y 'y' son objetos ciertos, entonces “x € S” denota que x es un miembro del conjunto S y “y ₡ S” denota que “y” no es un elemento de S.
Aquí existen muchos términos así que iremos explicando a medida que vayamos avanzando.
Antes que nada mencionemos al Operador Binario. OJO, no confunda, este operador NO tiene nada que ver con los números binarios en si. Se conoce como Operador Binario a cualquier “operador” que es usado para realizar una “operación” entre dos elementos.
Sabemos que algunos de los postulados más conocidos del Álgebra son:
Ley Asociativa. Esta ley dice que siendo * un operador binario, se dice que un conjunto cumple con la ley asociativa si:
(x*y)*z = x*(y*z)
para todo x, y, z miembros del conjunto.
Ley Conmutativa. Esta ley dice que siendo * un operador binario, se dice que un conjunto cumple con la ley conmutativa si:
x*y = y*x
para todo x, y miembros del conjunto.
Ley Distributiva. Esta ley dice que siendo * y • operadores binarios, se dice que un conjunto cumple con la ley distributiva si:
z*(x•y) = (z*x)•(z*y)
para todo x, y, z miembros del conjunto.
Elemento de identidad. Se dice que un conjunto tiene elemento de identidad con respecto a la operación binaria * si, siendo e la identidad, se cumple que:
e*x = x*e = x
para todo 'x' miembro del conjunto. O sea, en el álgebra de los números reales, el número 0 es elemento de identidad con respecto al operador binario + (suma) y 1 es el elemento de identidad con respecto al operador binario x (multiplicación).
El Álgebra de Boole es una sistema algebraico para el tratamiento de las relaciones lógicas (como la usada en los sistemas digitales). Está definida para un conjunto de elementos junto con sus operadores binarios '+' y '•' de tal forma que satisfagan los siguientes postulados:
Posee un elemento de identidad con respecto al operador + y éste es el 0 : A + 0 = 0 + A = A.
Posee un elemento de identidad con respecto al operador • y éste es el 1: A • 1 = 1 • A = A
Es conmutativo con respecto a + ya que: A + B = B + A
Es conmutativo con respecto a • ya que: A • B = B • A
• es distributivo sobre + ya que: A • (B + C) = (A•B)+(A•C)
+ es distributivo sobre • ya que: A + (B • C) = (A+B)•(A+C)
Para cada elemento x que pertenece a un conjunto, existe también en ese mismo conjunto un elemento x' llamado complemento de x tal que: (a) x + x' = 1 y (b) x • x' = 0.
Por último también debe satisfacer la existencia en el conjunto de al menos dos elementos x, y tal que x≠y... lo que está claro. Además, el álgebra de Boole también cumple con la ley asociativa pero no es un postulado como tal ya que éste puede ser demostrado a través de los mencionados.
OJO: '+' y '•' son los símbolos usados para expresar las operaciones binarias posibles en el álgebra de Boole y, aunque se escogieron porque tienen mucha semejanza con los usados en el álgebra de los números reales para la suma y la multiplicación, NO son exactamente iguales y ésto se hace absolutamente obvio en la segunda propiedad distributiva del postulado 3.
ÁLGEBRA DE BOOLE BIVALENTE
Éste es el caso particular que nos interesa ya que es el usado en los circuitos lógicos. Ésta se define como un conjunto de dos elementos {0, 1} y que cumplen las reglas para los operadores binarios + y • tal como se muestra en la siguiente tabla:
|
X |
Y |
X+Y |
X•Y |
X' |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
Éstas son las reglas de algunas de las operaciones lógicas, en particular de las conocidas como OR (para +), AND (para •) y NOT (para el complemento). Éstas son las tres operaciones lógicas básicas pero existen otras tal como el XOR u OR exclusivo pero de éstas se hablará luego. Las operaciones lógicas AND y OR tiene analogía en un circuito eléctrico. En el caso de la AND, visualicen un circuito con dos interruptores en serie y una carga, digamos un bombillo. Para que el bombillo se prenda, ambos interruptores deben estar cerrados. El circuito de la OR sería con los interruptores en paralelo. Si uno de ellos o ambos están cerrados, el bombillo se enciende.
La tabla anterior en la que se muestra la información es una forma ampliada de una tabla de la verdad. En realidad, la tabla de la verdad lo que muestra es el posible resultado que se puede generar de las distintas combinaciones de los valores posibles de las variables involucradas, en este caso, “x” y “y”, según una función u operación. Las tres primeras columnas de la tabla anterior reflejan la tabla de la verdad de la operación lógica OR. La primera, segunda y cuarta columna reflejan la tabla de la verdad de la operación lógica AND. Las tablas de la verdad son de gran ayuda sobre todo al momento de querer simplificar o entender funciones lógicas. Ya llegaremos a ello.
NOTA: Las tablas de la verdad de las distintas operaciones lógicas son algo que deben aprender perfectamente. En realidad no es difícil ya que solemos pensar de esa forma. Por ejemplo cuando decimos quiero café Y leche se entiende perfectamente que se quieren las dos cosas. Una AND. Solo se cumple si ambas cosas son ciertas. En el caso del OR en realidad hay una diferencia ya que nosotros gramaticalmente interpretamos un O refiriéndonos a que se cumple una cosa o la otra pero no ambas. Quiero una camisa Blanca O Negra. El OR presenta el caso de que si ambos son ciertos entonces el resultado también es cierto.
Se ve que la ley conmutativa es obvia en la tabla. La ley distributiva puede ser demostrada a partir de la misma. Vemos los elementos identidad. También se puede concluir que x + x' = 1 y x • x' = 0. Cumple con los postulados.
LEYES Y TEOREMAS BÁSICOS DEL ÁLGEBRA DE BOOLE
A continuación presento información recopilada de la Wikipedia. Por cierto que a los puntos siguientes sólo agregaría lo que acabo de mencionar al finalizar el punto anterior y las operaciones posibles con la identidad. (que luego se ven en la tabla en dualidad). Cito:
Leyes fundamentales
El resultado de aplicar cualquiera de las tres operaciones definidas a variables del sistema booleano resulta en otra variable del sistema, y este resultado es único.
Ley de idempotencia: A + A = A y A • A = A
Ley de involución: (A')' = A
Ley conmutativa: A + B = B + A y A • B = B • A
Ley asociativa: A + (B + C) = (A + B) + C y A • (B • C) = (A • B) • C
Ley distributiva: A + B • C = (A + B) • (A + C) y A • (B + C) = A • B + A • C
Ley de absorción: A + A • B = A y A • (A + B) = A
Ley de De Morgan: (A + B)' = A' • B' y (A • B)' = A' + B'
Principio de dualidad
El concepto de dualidad permite formalizar este hecho: a toda relación o ley lógica le corresponderá su dual, formada mediante el intercambio de los operadores unión (NOTA PERSONAL: el + ) con los de intersección (NOTA PERSONAL: el • ), y de los 1 con los 0.
|
Adición |
Producto |
|
|---|---|---|
|
1 |
A + A' = 1 |
A • A' = 0 |
|
2 |
A + 0 = A |
A • 1 = A |
|
3 |
A + 1 = 1 |
A • 0 = 0 |
|
4 |
A + A = A |
A • A = A |
|
5 |
A + B = B + A |
A • B = B • A |
|
6 |
A + (B + C) = (A + B) + C |
A • (B • C) = (A • B) • C |
|
7 |
A + B • C = (A + B) • (A + C) |
A • (B + C) = A • B + A • C |
|
8 |
A + A • B = A |
A • (A + B) = A |
|
9 |
(A + B)' = A' • B' |
(A • B)' = A' + B' |
FIN DE LA CITA.
Entonces, para resumir y concluir este apartado se podría decir que todos los postulados se resumen en:
(a) x + 0 = x ; (b) x • 1 = x
(a) x + x' = 1 ; (b) x • x' = 0
(a) x + y = y + x ; (b) x•y = y•x (conmutativo)
(a) x • (y + z) = xy + xz ; (b) x + (y • z) = (x + y) • (x + z) (distributivo)
y que de ellos pueden obtenerse (y probarse a través de demostraciones matemáticas) los 6 teoremas:
(a) x + x = x ; (b) x • x = x
(a) x + 1 = 1 ; (b) x • 0 = 0
(x')' = x (involución)
(a) x + (y + z) = (x + y) + z ; (b) x • (yz) = (xy) • z (asociativo)
(a) (x + y)' = x'•y' ; (b) (xy)' = x' + y' (de Morgan)
(a) x + xy = x ; (b) x(x + y) = x (de absorción)
Entiéndase que, igualmente a lo que estamos acostumbrados, xy es equivalente a decir x•y.
Si quieren, también pueden comprobar lo anteriormente dicho realizando la tabla de la verdad de los distintos casos.
Si por curiosidad desean ver como demostrar los teoremas a través de los postulados pueden revisar el libro “Lógica Digital y Diseño de Computadoras” de M. Morris Mano en sus páginas 42 y 43.
Prioridad del operador: La prioridad del operador al momento de evaluar una operación viene dado por: Primero lo que está dentro de paréntesis, segundo se realiza el operador NOT ( ' ), tercero el operador AND ( • ) y por último el operador OR ( + ).
Para más información del álgebra de Boole puede visitar este vínculo o este otro , ambas en la Wikipedia. Puede también encontrar información interesante de éste y muchos otros temas relacionados aquí.
FUNCIONES LÓGICAS
También conocidas como funciones Booleanas, no son más que expresiones formadas por variables binarias (o sea, que sólo pueden ser cero o uno), los operadores lógicos OR, AND y NOT como también los paréntesis y el signo de igual. El orden en el que se realizan las operaciones viene dada por la prioridad del operador que comentamos al final del apartado anterior.
Suponga lo siguiente: usted tiene un bombillo en su casa. Éste contiene dos interruptores. Entendiendo que la posición del interruptor en encendido se interpreta como un cierto o “1” y que el bombillo encendido también se entiende por un cierto o “1”, si usted quiere que el bombillo se encienda si y sólo si ambos interruptores están en la posición de encendido, usted podría definir una función lógica del problema de la siguiente forma:
F = xy
donde F es una función de Boole cuyo resultado sólo puede ser '1' (encendido) ó '0' (apagado) y que muestra el estado del bombillo para las dos variables binarias 'x' y 'y' que serían los interruptores. Si creamos la tabla de la verdad de esta función tenemos que:
|
X |
Y |
F |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
y esto es precisamente lo que queríamos obtener. El bombillo se encenderá si ambos interruptores están encendidos.
Veamos otro ejemplo. F1 = xyz'
Esto es una función de Boole representada por una expresión algebraica. Ésta la podemos representar también por medio de la tabla de la verdad.
|
X |
Y |
Z |
F1 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
Se ve que F1 será 1 si x = 1, y = 1, z = 0 (z' = 1). Las tablas de la verdad de las funciones de Boole contendrán siempre 2n combinaciones de unos y ceros de las n variables incluida en la función y una columna que mostrará para que combinación el resultado es uno o cero. En el caso anterior teníamos 3 variables or lo que necesitamos 8 combinaciones (23).
Consideremos ahora los siguientes dos casos: F2 = x + y'z y F3 = x'y'z + x'yz + xy'
El la siguiente tabla de la verdad se muestran para que casos las funciones F2 y F3 se hacen uno.
|
X |
Y |
Z |
F2 |
F3 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
Ok, pero existen varias expresiones algebraicas capaces de obtener el mismo resultado con las mismas variables. ¿Qué quiere decir esto? Que yo puedo tener dos funciones de Boole con las mismas variables pero organizadas de otra forma (incluso puede contener menos variables) tal que el resultado de ambas funciones de Boole sea el mismo. De hecho ésta es una de las aplicaciones más importantes que se pueden obtener del álgebra de Boole y consiste en reducir o “simplificar” una función. De esta forma forma podríamos realizar el diseño de nuestro circuito lógico de una forma más compacto y con el uso de menos compuertas. Fíjese en el siguiente ejemplo:
F4 = xy' + x'z
Si realiza la tabla de la verdad de esta función observará que el resultado es el mismo que para la función F3. F4 será uno o cero para la misma combinación de X, Y y Z que hacen uno o cero la función F3.
Como ya se mencionó, las funciones lógicas pueden resumirse, hacerse más sencillas. De esta forma al realizar el circuito se usarán menos compuertas. Lás formas de simplificar dichas funciones es tema de los próximos temas. Una función lógica puede ser transformada de una expresión algebraica a un diagrama compuesto por compuertas lógicas AND, OR y NOT. Por ahora veamos algunos conceptos básicos de las compuertas lógicas (que es el punto a seguir) y al finalizarlo les mostraré como se expresa una función lógica en un diagrama de bloque formado por compuertas.
COMPUERTAS LÓGICAS
Los sistemas digitales electrónicos se llaman circuitos lógicos ya que realizan manipulaciones lógicas. Cualquier información deseada en un sistema de control puede ser obtenida a través de la combinación de varias operaciones lógicas. Como ya sabemos, las operaciones lógicas básicas son AND, OR y NOT y son precisamente éstas las que se implementan en los circuitos lógicos, ésto gracias al uso de las compuertas lógicas correspondientes. Una compuerta lógica no es más que un diseño de circuitería electrónico capaz de reproducir el comportamiento de las operaciones lógicas.
Existen compuertas lógicas para AND, OR, NOT y otras operaciones lógicas como la XOR u OR Exclusivo. La XOR se diferencia de la OR en que si sus dos entradas son '1' entonces el resultado será '0' (la cual es la forma más natural en la que nosotros pensamos gramaticalmente... algo puede ser Blanco o Negro pero no ambos). El símbolo para expresar XOR viene dado por signo + inscrito en un círculo. La tabla de la verdad de función XOR es:
|
A |
B |
|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
También existen compuertas para las operaciones lógicas NAND (que es una AND con un inversor (NOT) a la salida), la NOR (una OR con un inversor a la salida) y la XNOR (o NOR exclusivo representado por un punto inscrito en un círculo, que no es más que una XOR con un inversor a la salida) entre algunas otras pero diría que las ya mencionadas son las más importantes.
A continuación mostraré los símbolos que representan las compuertas descritas:
|
Nombre |
Símbolo |
|
AND |
|
|
OR |
|
|
NOT |
|
|
NAND |
|
|
NOR |
|
|
XOR |
|
|
XNOR |
|
ATENCIÓN: A excepción de la NOT, el resto de las compuertas pueden tener más de dos entradas.
Sabiendo ésto, veamos ahora como se representarían algunas de las funciones de las que hablamos antes pero diagramadas con las compuertas. En particular veremos las funciones F = xyz' y F4 = xy' + x'z. En ese orden:
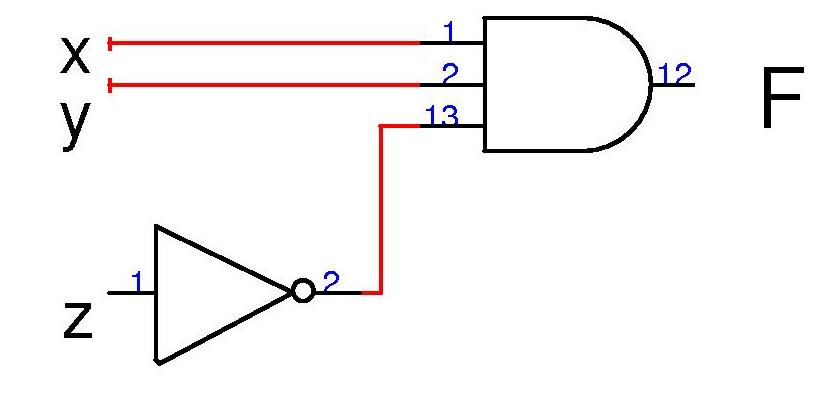
y el otro sería:
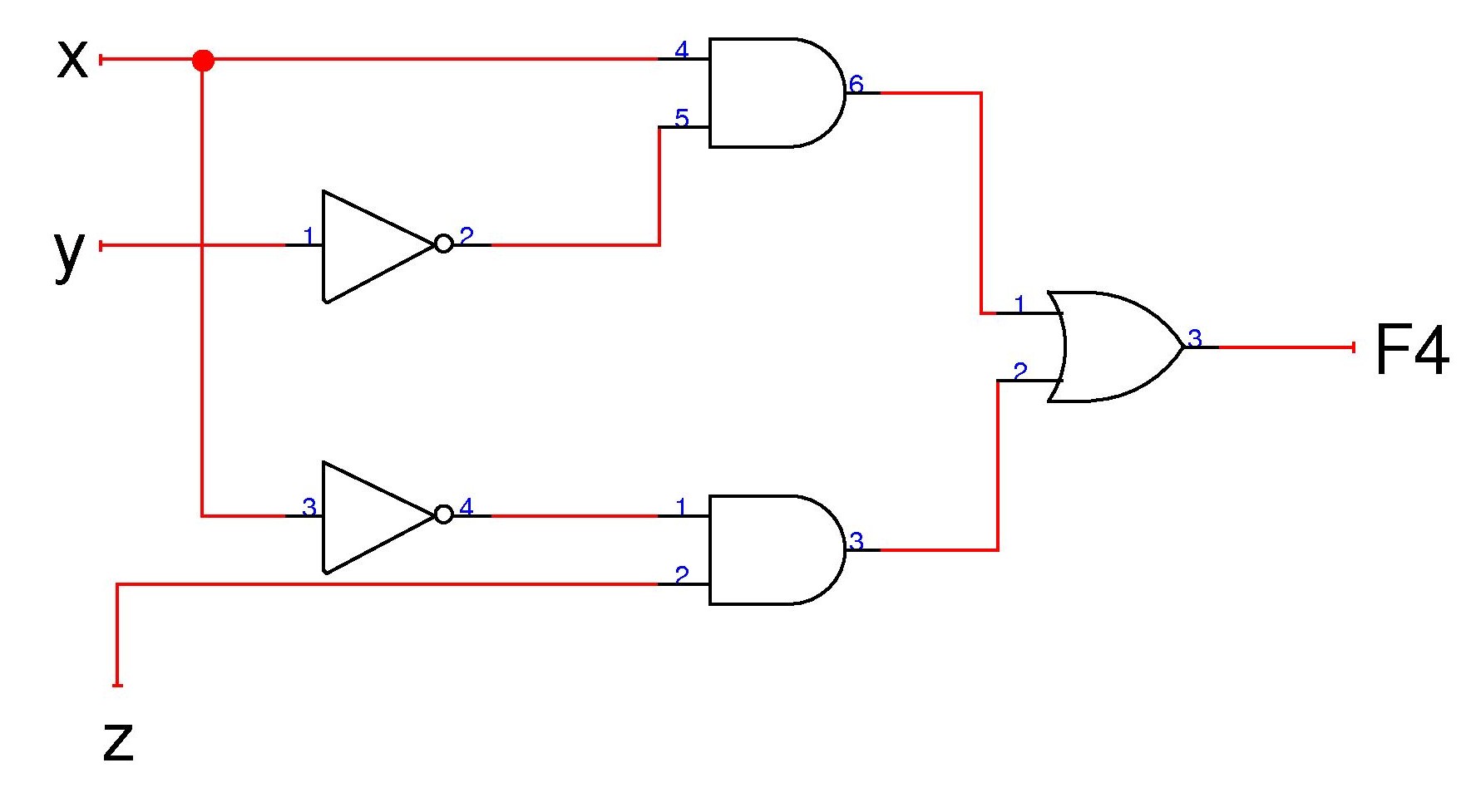
Esto
es todo por este tema. Para el próximo hablaremos de
Simplificación de funciones por algebra
de Boole. Tabla de la verdad. Formas canónicas.