Hasta ahora siempre hemos visto en nuestras tablas de la verdad los casos para cuando una combinación cualquiera en las entradas hacen nuestra salida del circuito cierta (un 1), y solíamos asumir que el resto de ellas eran falsas (cero). Ésto no es siempre cierto. Al momento de diseñar nuestros circuitos se nos pueden presentar casos en los que una combinación en la entrada no sea de nuestro interés. Estas condiciones que no nos importan se conocen como “condiciones irrelevantes” o también con la frase inglesa “don't care”. Estas condiciones suelen expresarse en las tablas de la verdad con una 'X' y al momento de realizar la simplificación de la función podemos asumir que este valor es uno o cero según más nos convenga (lo que haga la expresión aún más reducida). Incluso podemos sencillamente ignorar este valor si no obtenemos ningún beneficio de él. Pero me imagino que se preguntarán, ¿Cómo es eso de una combinación en la entrada que no nos importa? Bien, un ejemplo clásico es que al circuito se le entregue para procesar un número en BCD. Ya sabemos que el código BCD usa 4 bits para expresar los 10 dígitos decimales pero de esta forma sobran otras seis combinaciones que no se usan (1010, 1011, 1100, 1101, 1110 y 1111). Pues bien, si nuestro circuito procesará este número en BCD, en nuestra tabla de la verdad tendríamos seis casos que no nos importan ya que sencillamente nunca ocurrirán.
Veamos un ejemplo también clásico para ejemplificar ésto. Supongamos que se pide diseñar un circuito que debe reconocer cuando un número entre 1 y 9 es primo. Para este caso tendríamos una tabla de la verdad como la que sigue:
|
A |
B |
C |
D |
Out |
|
0 |
0 |
0 |
0 |
X |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
X |
|
1 |
0 |
1 |
1 |
X |
|
1 |
1 |
0 |
0 |
X |
|
1 |
1 |
0 |
1 |
X |
|
1 |
1 |
1 |
0 |
X |
|
1 |
1 |
1 |
1 |
X |
Se observa que en la entrada que representaría el valor decimal 0 se coloca X ya que este caso no está dentro de los presentados en el enunciado (entre 1 y 9). De forma análoga, los casos del 10 al 15 tienen X por la misma razón. En ciertas bibliografías muestra la expresión:
d(A,B,C,D) =∑ (0,10,11,12,13,14,15)
para representar los casos que no importan (letra “d” por don't care).
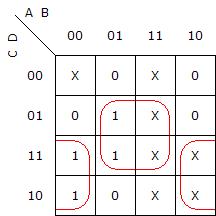
Bien, ahora, veamos como se vería un mapa derivado de esta tabla de la verdad:
|
CD\AB |
00 |
01 |
11 |
10 |
|
00 |
X |
0 |
X |
0 |
|
01 |
0 |
1 |
X |
0 |
|
11 |
1 |
1 |
X |
X |
|
10 |
1 |
0 |
X |
X |
Ok. Vemos que la mejor forma de considerar los casos irrelevantes es haciendo que donde va m0, m12, y m14 haya cero y en el resto un uno. Así podremos hacer el menor número de grupos y a la vez los hacemos lo más grandes posibles, tal y como vemos en el siguiente mapa:

Así obtendríamos la función de salida:
F = BD + B'C
Veamos otro ejemplo. Sabiendo que su circuito recibirá una entrada BCD, el mismo debe determinar cuando el número de entrada es par. (Aunque según para algunos lo que diré a continuación no es cierto, asuma para este ejemplo que que el cero es par).
|
A |
B |
C |
D |
Par |
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
X |
|
1 |
0 |
1 |
1 |
X |
|
1 |
1 |
0 |
0 |
X |
|
1 |
1 |
0 |
1 |
X |
|
1 |
1 |
1 |
0 |
X |
|
1 |
1 |
1 |
1 |
X |
De esa tabla de la verdad podemos concluir el siguiente mapa:
|
CD\AB |
00 |
01 |
11 |
10 |
|
00 |
1 |
1 |
X |
1 |
|
01 |
0 |
0 |
X |
0 |
|
11 |
0 |
0 |
X |
X |
|
10 |
1 |
1 |
X |
X |
Se hace bastante fácil de ver que la mejor forma de agrupar es:
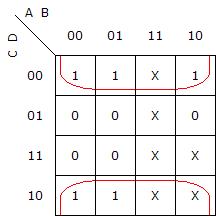
que
se resume como: Par = D', conclusión bastante obvia según
la tabla de la verdad donde se ve que para los casos que importan, la
salida es igual al bit menos significativo negado (siempre que D=1 la
división entre dos daría resto de 1).
Si lo desean, para practicar, tome los ejemplos y ejercicios del capítulo pasado y reemplacen algunos ceros por X a su antojo y vean los diferentes resultados que pueden obtener.
UNIVERSALIDAD DE LAS COMPUERTAS NAND Y NOR
Las compuertas NAND y NOR son llamadas universales debido a que a través de la combinación de éstas pueden obtenerse las AND, OR y NOT. Ésto quiere decir que cualquier circuito puede implementarse (si bien es cierto que no necesariamente de forma más eficiente) con sólo compuertas de alguno de esos tipos. Una compuerta NAND no es mas que una AND con una NOT a la salida. Análogamente, una compuerta NOR es una OR con una NOT en la salida.
Voy a aprovechar unos gráficos que conseguí en Internet para mostrar como pueden combinarse las NAND y las NOR para crear los distintos tipos de compuertas que usamos en nuestras funciones booleanas y también para mostrar como se expresan gráficamente esas compuertas.
|
FORMA NORMAL |
NAND |
NOR |
|
|
|
|
|
|
|
|
|
|
|
|
OJO: Recuerden que colocar una raya sobre la variable indica que ésta está negada, como si pusiéramos el tilde (').
NOTA: Existen otras compuertas que tienen las mismas funcionalidades que las NAND y las NOR. Para el caso de las NAND tenemos la compuerta OR con todas sus entradas negadas (el símbolo es el mismo de la or pero con un círculo en cada entrada indicando que son negadas). Claro, sabemos por Morgan que A'+B' = (AB)'. De forma análoga, la compuerta NOR puede verse como una compuerta AND con todas sus entradas negadas (el símbolo es una AND con círculos en todas sus entradas.).
Se ve que la única diferencia entre una NAND y una AND y entre una OR y una NOR es el círculo que se encuentra en el lado de la salida de la compuerta. Los casos más interesantes son para la construcción de una AND con NOR y de una OR con NAND en los que se ve la aplicación del teorema de Morgan.
En realidad, al menos en los circuitos integrados, los circuitos se construyen con mucha más frecuencia con compuertas NAND y NOR que con las AND, OR y NOT. Esto es debido a que esas compuertas son mucho más fáciles de construir y requieren de la integración de menos transistores.
Entonces, todo circuito puede ser llevado a formas estructuradas por puras compuertas NOR o puras compuertas NAND. Si se quiere implementar con compuertas NAND se lleva la función a una forma de suma de productos y se niega dos veces ya que sabemos, por el principio de involución, que así obtenemos la misma función original. Al momento de negar hacemos uso del Teorema de Morgan . Si en cambio se quiere ver con compuertas NOR debe llevarse a una forma de producto de sumas y negar dos veces.
Ejemplos: Implementar F = AB + CD + E con compuertas NAND.
F = [(AB+CD+E)']' = [(AB)'.(CD)'.E']'
que es una implementación con 5 compuertas NAND. El gráfico se hizo en clase. No lo coloco aquí por falta de tiempo para hacerlo.
Veamos que pasa si se pide implementar con NOR. Tenemos F = (A+B)(C+D)E, que se ve que ya está en forma de producto de términos sumas. De hecho, esta función es la dual de la anterior. Al aplicar involución obtenemos: F = [(A+B)'+(C+D)'+E']'. Ver la clase para el diagrama del mismo.
Estos dos ejemplos tienen sólo dos niveles de ejecución. Las entradas van a una compuerta y las salidas de éstas van a su vez a la entrada de otra. Si la salida del segundo nivel fuese a otra compuerta, entonces se diría que tiene tres niveles de ejecución.
NOTA: Esto ya es de clases pasadas, pero recuerden que si les digo que F(A,B,C)=∑(0,6), F' será la suma de los términos mínimos que son cero en la tabla de la verdad o en el mapa de K.
Para la próxima clase veremos el tema 6: Simplificación de funciones por el método de Quine-Mc Cluskey. Dispositivos lógicos programables combinacionales.