SIMPLIFICACIÓN DE
FUNCIONES POR EL MÉTODO DE LOS MAPAS DE KARNAUGH
Anteriormente
comentamos que habían otras formas de simplificar una función
aparte de la simplificación algebraica. Otra manera de
simplificar funciones es representándolas en lo que se conoce
como mapas de Karnaugh. Éste constituye
un método sencillo y apropiado para la minimización de
funciones lógicas. El tamaño del mapa depende del
número de variables, y el método de minimización
es efectivo para expresiones de hasta 6 variables. Por supuesto que
siempre podrán resolverse las simplificaciones
por teoremas. Sin embargo, mucha gente considera que resulta más
fácil visualizar las simplificaciones si se presentan
gráficamente. Como ya se dijo, los mapas de Karnaugh pueden
aplicarse a dos, tres, cuatro, cinco y seis variables ya que para más
variables, la simplificación resulta tan complicada que
conviene en ese caso utilizar teoremas mejor. Entonces, el mapa
de Karnaugh es un método gráfico que se utiliza para
simplificar una función lógica y así facilitar
el diseño del correspondiente circuito lógico, todo en
un proceso simple y ordenado.
Obtener la
función de un Mapa de Karnaugh es el procedimiento inverso a
la de la realización del mapa. Un término de la función
coloca uno o mas "unos" en el mapa de Karnaugh. Tomar esos
unos, agrupándolos de la forma adecuada, nos permite obtener
los términos de la función. Utilizaremos los Mapas de
Karnaugh para obtener una función mínima. Una expresión
es mínima si no existe otra expresión equivalente que
incluya menos términos y no hay otra expresión
equivalente que conste con el mismo número de términos,
pero con un menor número de literales. Pueden existir varias
expresiones distintas, pero equivalentes, que satisfagan esta
definición y tengan el mismo número de términos
y literales.
La
minimización de funciones sobre el mapa de Karnaugh se
aprovecha del hecho de que las casillas del mapa están
arregladas de tal forma que entre una casilla y otra, en forma
horizontal o vertical existe ADYACENCIA LOGICA. Esto quiere decir que
entre una casilla y otra sólo cambia una variable.
Definimos
los “términos mínimos adyacentes” desde el
punto de vista lógico como dos términos mínimos
que difieren sólo en una variable. Agrupando casillas
adyacentes obtenemos términos que eliminan las variables que
se complementan, resultando ésto en una versión
simplificada de la expresión.
El
procedimiento es el de agrupar "unos" adyacentes en el
mapa. Cada grupo corresponderá a un término producto, y
la expresión final dará un OR (suma) de todos los
términos producto. Se busca obtener el menor número de
términos productos posible.
Veamos
ahora algunos ejemplos ya que creo que la mejor forma de entender
este concepto es con ellos.
1.-
Simplificar la función de dos variables F=A'B+AB'+AB
Lo
primero que hay que hacer es representarlo en un mapa de dos
variables. La forma de hacerlo es similar a una tabla. Veamos como
sería la tabla de la verdad:
-
|
A
|
B
|
F
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
Para un
mapa de dos variables, el concepto sería algo como:
-
|
A \ B
|
0
|
1
|
|
0
|
m0
|
m1
|
|
1
|
m2
|
m3
|
OJO: Puse
el signo “\” por comodidad pero en realidad es una
línea completa desde la esquina superior izquierda hasta la
inferior derecha que divide esa celda en dos triángulos
iguales. Las variables con las que se está trabajando se
colocan en cada una de esas divisiones. En este caso quiero hacer ver
que la A es la columna y la B es la fila. De ahora en adelante lo
mostraremos siempre así pero en realidad debería verse
así:
Pues
bien, mn representa los términos mínimos.
Si tuviésemos la función expresada en forma canónica
según sus términos mínimos ya sabríamos
exactamente donde colocar todos los unos. Observen también que
en el mapa se ve 0's y 1's tanto en la columna como en la fila. La
columna indicaría cuando A=0 (también puede colocarse
A' en vez del 0) y cuando A=1 (puede colocarse A). Sabiendo ésto,
y con ayuda de la tabla de la verdad que nos indica cuales son los
casos en los que se hace uno la función, veamos ahora como
sería con un mapa de Karnaugh:
-
O incluso
podrían hacer algo como:
-
O
sea, que para llenar la tabla, pongo un uno en todos los términos
mínimos que contenga la función (que para la función
F=A'B+AB'+AB son m1, m2 y m3
respectivamente) o sencillamente donde la tabla de la verdad me
indique [que son los grupos (A,B) = (0,1), (1,0) y (1,1)]. Dicho
ésto, creo que ya pueden visualizar bien la forma en la que se
hace el mapa. Continuemos.
Una vez hecho el mapa, debemos
marcar las regiones contiguas que manejen 1's. En el siguiente dibujo
vemos cómo se marcan dos regiones. Estas regiones son las
simplificaciones. Como la región azul involucra solamente a la
B, eso representa. La región roja, por su parte, involucra
solamente a la A.
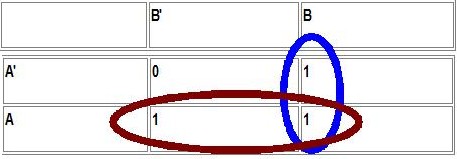
Una
vez definidas las regiones o “agrupaciones”, se escribe
la función simplificada y en este caso es F=A+B (Que es la
respuesta obvia ya que el único 0 que contiene la función
es M0 y dicho término máximo es A+B). Viendo
la tabla de la verdad, también se deduce que la operación
es una OR.
Las
“agrupaciones” siempre se hacen en forma de rectángulo.
En general, si tenemos una función con n variables :
Un rectángulo que
ocupa una celda equivale a un término con n variables.
Un rectángulo que
ocupa dos celdas equivale a un término con n-1 variables.
Un rectángulo que
ocupa 2n celdas equivale al término de
valor 1.
Todos
los rectángulos o agrupaciones contendrán un número
par de celdas (en realidad con 2n celdas) con la
única excepción de cuando es una celda única.
Por lo tanto, para encontrar expresión más simplificada
se debe:
Minimizar el
número de rectángulos que se hacen en el mapa de
Karnaugh, para minimizar el número de términos
resultantes.
Maximizar el
tamaño de cada rectángulo, para minimizar el número
de variables de cada término resultante.
Veamos
otro ejemplo: Simplificar la
función de tres variables F=A'B+AB'C+C'
Lo primero que hay
que hacer es representarlo en un mapa de Karnaugh de tres variables.
En el caso de 3 variables la forma genérica sería algo
como:
-
|
A \ BC
|
00
|
01
|
11
|
10
|
|
0
|
m0
|
m1
|
m3
|
m2
|
|
1
|
m4
|
m5
|
m7
|
m6
|
Ok,
ponga muchísima atención acá. En las tablas para
tres variables, colocamos una variable sóla (ya sea en la
columna o en la fila) y las otras dos variables juntas en el otro
extremo. Yo lo coloco así por costumbre pero como usted lo
ordene no cambiará el resultado. OBSERVE
con especial atención la forma en la que varía los
números en el mapa. En el caso de la fila que contiene a BC,
los bits que contienen NO incrementan en forma normal. En vez de ello
el cambio se hace de forma tal que los valores adyacentes reflejen
únicamente el cambio de un bit (algo así al estilo del
código Gray o reflejado que vimos en capítulos
anteriores). Esto DEBE HACERSE ASÍ. De lo contrario el mapa no
serviría ya que celdas adyacentes podrían contener
cambios de más de una variable lo cual es impermisible.
Observen también que debido a esta característica los
términos mínimos en las celdas no cambian incrementando
naturalmente en decimal. Se ve que en la fila de A' se encuentran m0,
m1, m3, y m2 respectivamente y en
ese extricto orden. NOTA: Un tip. El
término mínimo que debe ir en cada celda se puede
calcular fácilmente convirtiendo los bits ABC a decimal. Por
ejemplo, en la celda en la que la combinación de los bits para
ABC es 011 (cuyo valor decimal es 3), va rellena con m3.
Esta propiedad se cumple siempre y lo veremos en los casos con más
variables.
Dicho
esto continuemos. Aquí no realizaré la tabla de la
verdad. En vez de ello colocaré los unos directamente sobre el
mapa. Si usted quiere puede hacer la tabla de la verdad o llevar la
función a su forma canónica. Yo sencillamente no lo
hago para ahorrar tiempo ya que en este punto, esos temas ya deben
ser dominados por ustedes. En todo caso el resultado de la función
en sus formas canónicas simplificadas es
F(A,B,C)=∏(1,7)=∑(0,2,3,4,5,6)
-
|
A \ BC
|
00
|
01
|
11
|
10
|
|
0
|
1
|
0
|
1
|
1
|
|
1
|
1
|
1
|
0
|
1
|
Coloqué
los unos donde correspondía y ahora debemos buscar las
regiones que nos indiquen la función simplificada. Lo primero
que debemos observar es que las regiones pueden agruparse de los
extremos del mapa, como la región azul que vemos a
continuación:
Esta
región representa a C'. ¿Por qué queda C'?
Observe que el rectángulo de 4 celdas son comunes a C=0. (Para
facilitar el entendimiento de este punto, coloque A en amarillo en el
borde izquierdo para cuando A=1 y coloqué unas llaves que
indican cuando B=1 y C=1). Se ve que el rectángulo rodeado por
azul es C' (La llave con C no tiene ningún caso allí) y
se ve que no importan los valores de A ni de B ya que están
complementados (0 ó 1 en ambas variables). Vemos
también que queda un bit en A'BC (que está en rojo) y
uno en AB'C (en amarillo), pero siempre conviene agruparlo lo más
posible, en regiones cuyas celdas sean potencias de 2. En este
caso, los agrupamos con el 1 contiguo, para que la región
quede como A'B (ya que la elipse roja está sobre A' y bajo B
-vea la llave) y AB' (analícelo) respectivamente. Así,
la función resultante sería F=A'B+AB'+C'.
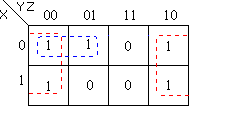
Veamos otro caso. Simplificar la
función de cuatro variables F(A,B,C,D)=∑(0,2,3,5,7,8,10,13)
En los casos de 4 variables podemos
organizar de la siguiente forma:
-
|
AB \ CD
|
00
|
01
|
11
|
10
|
|
00
|
m0
|
m1
|
m3
|
m2
|
|
01
|
m4
|
m5
|
m7
|
m6
|
|
11
|
m12
|
m13
|
m15
|
m14
|
|
10
|
m8
|
m9
|
m11
|
m10
|
Note nuevamente la variación
en las filas y columnas. Sólo un bit cambia en las
adyacencias. FÍJESE muy bien como
quedaron organizados los términos mínimos. Vea y
deduzca que si combina los bits ABCD y convierte a decimal, verá
que la celda correspondiente contiene el término mínimo
que explicamos anteriormente que debería contener. Por ejemplo
si AB,CD=10,11, (1011)2=11 y en dicha celda está
m11.
Lo primero que hacemos es vaciar la
función al mapa. Como ya tenemos la forma canónica, el
vaciado es directo. Observe como queda el mapa.
-
|
AB \ CD
|
00
|
01
|
11
|
10
|
|
00
|
1
|
0
|
1
|
1
|
|
01
|
0
|
1
|
1
|
0
|
|
11
|
0
|
1
|
0
|
0
|
|
10
|
1
|
0
|
0
|
1
|
Ahora, lo siguiente es agrupar las
variables en regiones. La primera región agrupada son las
esquinas (en rojo). Esta agrupación representa B'D' ya que los
valores comunes son B=0 y D=0. A y C tienen ambos valores, o sea,
están complementados. Como ejercicio muestre este mapa con las
llaves indicando donde las variables son 1 tal como mostré el
caso anterior. No lo hago yo aquí porque me consume mucho
tiempo. Sigamos. La siguiente región la agrupo con los 1's en
verde y esta agrupación representa A'CD. Pude hacer el grupo
con el 1 a la derecha, pero hubiera significado agrupar un 1 ya
agrupado (que, como vimos, a veces es requerido para simplificar aún
más la expresión), y dejar otro 1, aún no
agrupado, por agrupar. Así que se agrupa de esta forma para
obtener menos términos. Los 1's que quedan hasta este momento,
en azul, pueden agruparse juntos. Esto representa a BC'D. Por lo
tanto la función queda: F=B'D'+A'CD+BC'D.
Es importante notar que se puede
agrupar otra region con un 1 verde y uno azul y representaría
A'BD. Esta región es una simplificación adicional
válida, que pudo haberse manejado e incluso agregado a la
función. En ocasiones, habrá varias formas de agrupar a
los 1's. Todas son válidas, y representan soluciones
equivalentes. Sin embargo, hay que cuidar de siempre agrupar las
regiones lo más grandes posibles, y cuidando de agrupar a los
1's de manera que se repitan lo menos posible. Como esos “unos”
ya fueron agrupados no requieren volver a serlo.
Entonces
los pasos a seguir para simplificar una función son:
1.
Convertir la expresión a una suma de productos si es
necesario. Ésto se puede realizar de varias maneras:
Llevándola
algebraicamente a su forma canónica.
Construyendo una tabla
de verdad, trasladando los valores al mapa de Karnaugh.
2.
Cubrir todos los unos del mapa mediante rectángulos de
2n elementos. Ninguno de esos rectángulos
debe contener ningún cero.
Para minimizar el número
de términos resultantes se hará el mínimo
número posible de rectángulos que cubran todos los
unos.
Para minimizar el número
de variables se hará cada rectángulo tan grande como
sea posible. Ejemplo:
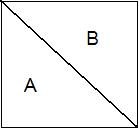
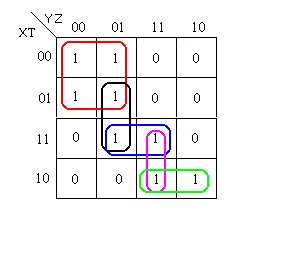
Véase
que en este caso se ha unido la columna izquierda con la derecha para
formar un único rectángulo y que el “uno”
en 001 se ha emparejado con el “uno” de al lado con la
idea de reducir ese término en un literal.
3.
Encontrar la suma de productos mínima. Ojo, como ya
se dijo, podemos encontrarnos con que puede haber más de una
suma de productos e incluso casos en que tengamos dos reducciones con
el mismo número de términos y literales siendo ambas
válidas.
En nuestro ejemplo
tenemos F(X, Y, Z) = Z’ + X’Y’
. Nótese que las
variables resultado son las que tienen un valor común en cada
rectángulo.
Cada rectángulo
representa un término. El tamaño del rectángulo
y el del término resultante son inversamente proporcionales,
es decir que, cuanto más largo sea el rectángulo menor
será el tamaño del término final.
Cuando tenemos distintas
posibilidades de agrupar rectángulos hay que seguir ciertos
criterios:
Localiza
todos los rectángulos más grandes posibles, agrupando
todos los unos. Estos se llamarán implicantes primos.
Si alguno de los
rectángulos anteriores contiene algún uno que no
aparece en ningún otro rectángulo entonces es un
implicante primo esencial. Éstos han de aparecer en el
resultado final de manera obligatoria.
El resto de los
implicantes primos se podrán combinar para obtener distintas
soluciones.
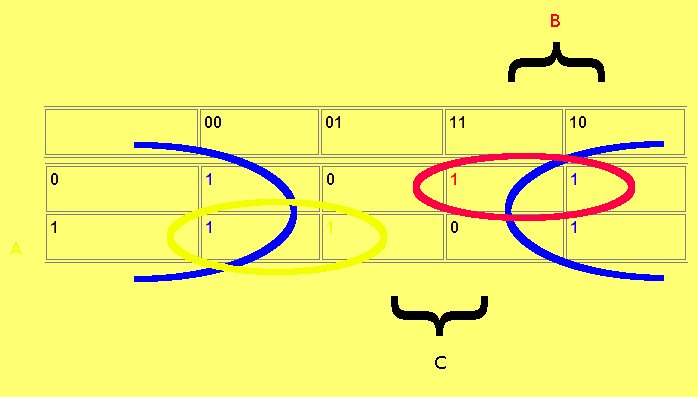
Véase
este ejemplo que ilustra lo dicho. Aquí los implicantes primos
son cada uno de los diferentes rectángulos obtenidos. Los
implicantes primos esenciales son el rectángulo rojo y el
verde, por contener “unos” que no son cubiertos por otros
rectángulos. Así todas las posibles soluciones han de
contener estos dos implicantes.
La
mejor solución, por ser la que usa menos términos y
menos literales es: F( X, Y, Z, T ) = X’Y’
+ XYT’ + XZT
Ejemplo.
Para la función:
F=A'B'C'D'+A'BC'D'+ABC'D'+AB'C'D'+A'BC'D+ABC'D+AB'C'D+ABCD+AB'CD+A'B'CD'+A'BCD'+ABCD'+AB'CD'
el
mapa es:
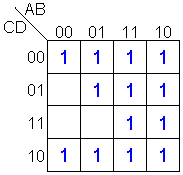
Supongamos
por un momento que agrupamos los "unos" del mapa de
Karnaugh como se muestra en la siguiente figura:
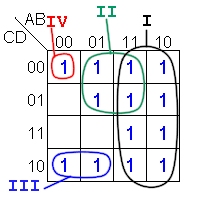
Según
esto tenemos cuatro términos que son:
término
I : agrupa 8 unos y es de una variable. Ésta es A. Este
término es un implicante primo esencial.
término
II : agrupa 4 unos y es de dos variables. Éstas son BC con C
negado. Es un implicante primo esencial.
término
III : agrupa 2 unos y es de tres variables. Éstas son ACD con
A y D negados. NO es un implicante primo.
término
IV : agrupa sólo un 1 y es de cuatro variables que son ABCD
todos negados. Éste, NO es un implicante primo.
Esa
forma de organizar el mapa NO contiene ningún implicante primo
que NO sea esencial.
Puede
verse que a medida que agrupamos mayor cantidad de "unos",
el término tiene menos literales. El agrupamiento se hace con
una cantidad de "unos" que son potencias de 2. Así
agrupamos 2 minterm's, 4 minterm's y 8 minterm's. Cada vez que
aumentamos el rectángulo, el término va eliminando una
variable. En una función de 4 variables, un término que
tenga un sólo "uno" tendrá las cuatro
variables. De hecho es un término canónico. Al agrupar
dos minterm's eliminaremos una variable y el término quedará
de tres variables. Si agrupamos cuatro "unos" eliminaremos
dos variable quedando un término de dos variables y finalmente
si agrupamos ocho "unos" se eliminaran tres variable para
quedar un término de una única variable. Todo esto se
debe a la adyacencia entre casillas y cada vez que agrupamos, se
eliminan las variables que se complementan.
En
este ejemplo obtenemos F=A'B'C'D'+A'CD'+BC'+A
Pero
en realidad, ésta no es la función mínima...
¿cierto? El mismo mapa podemos agruparlo de otra forma y
obtener:
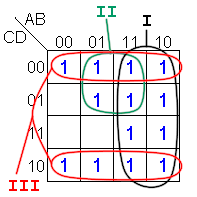
Ésta
forma de agruparlos nos da como resultado: F=D'+BC'+A que sí
es expresión mínima. Es importante que al "tomar"
un uno, se agrupe con todos los unos adyacentes, aunque éstos
ya sean parte de otros grupos. Fíjense que el minterm en
ABCD=(1100)2 es común a los
tres términos. Aquí, los tres grupos son implicantes
primos esenciales por lo que todos deben ir incluidos en la función
simplificada.
Vamos
de nuevo. Recuerden que para simplificar funciones
utilizando mapas de Karnaugh hay que tener en cuenta que:
Podemos
concluir que cada casilla (minterm) en un mapa de Karnaugh de n
variable tiene n casillas adyacentes lógicamente, o sea,
que se diferencian en las adyacencias por una sola variable (se
complementan). Esta información es de gran utilidad en los
casos de 5 y 6 variables.
Al
combinar las casillas en un mapa de Karnaugh, agruparemos un número
de minterm's que sea potencia de dos. Así, al agrupar dos
casillas eliminamos una variable, al agrupar cuatro casillas
eliminamos dos variables, y así sucesivamente. De hecho
podemos concluir que al agrupar 2n casillas,
eliminamos n variables.
Debemos
agrupar tantas casillas como sea posible; cuanto mayor sea el grupo,
el término producto resultante tendrá menos literales.
Es importante incluir todos los "unos" adyacentes a un
minterm que sea igual a uno.
Para
que hayan menos términos en la función simplificada,
debemos formar el menor numero de grupos posibles que cubran todas
las casillas (minterm's) que sean iguales a uno. Un "uno"
puede ser utilizado por varios grupos, no importa si los grupos se
solapan. Lo importante es que si un grupo está incluido
completamente en otro grupo, o sus "unos" están
cubiertos por otros grupos, no hace falta incluirlo como término.
Veamos
otro caso en el que repasamos lo que significa “términos
implicantes”. En el siguiente mapa de Karnaugh:
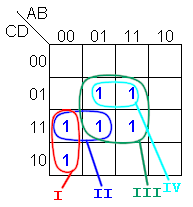
Los términos I, II y III son
implicantes primos.
El término IV no es implicante
primo.
Los términos I y III son
implicantes primos esenciales.
El término II no es un
implicante primo esenciales.
La función se obtiene con los
términos I y III
Mapas de
Karnaugh con 5 y 6 variables
Los ejemplos anteriores se realizaron con
funciones de hasta 4 variables. Para mapas de Karnaugh de 5 y 6
variables el procedimiento es esencialmente el mismo y sólo
hay que recordar que un término mínimo tiene adyacente
a otro minterm, tanto en forma horizontal o vertical, qué
muestra diferencia en una sola variable.
Veamos a continuación el caso de 5
variables. Aquí hay 25 = 32 posibilidades. Una de
las formas de ver el mapa es:
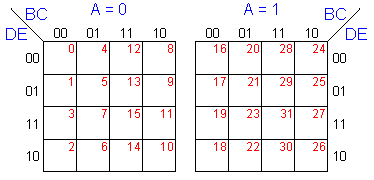
Ésta
será la forma que nosotros usemos. Se observa que se separan
los casos para A=0 y A=1 para hacerlo más fácil de
entender y que en las adyacencias sólo una variable cambia.
Todos los números en las celdas hacen referencia a los
términos mínimos. También debe saber que, tanto
en este caso como en el de 6 variables, la adyacencia también
se cumple para las mismas celdas de los cuadros que se encuentren al
lado tanto horizontal como verticalmente (Sólo
horizontal en 5 variables y ambos sentidos en 6). O sea, el término
mínimo 31 es adyacente al 15. De la misma forma los términos
mínimos 31 y 30 son adyacentes a los 15 y 14 respectivamente.
Se ve también que, al igual que en los otros casos, los
términos mínimos que corresponden a cada celda pueden
calcularse convirtiendo el número binario de la respectiva
combinación ABCDE. Por ejemplo, para ABCDE=(10110)2
=22, el término mínimo en la celda es el m22.
Supongamos
el siguiente caso: Simplificar la función
F=∑
(0,2,8,11,15,18,20,21,27,28,29,31)
Colocando un
uno en los términos mínimos correspondientes, tenemos
que:
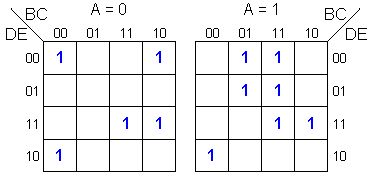
De
forma análoga a lo que hemos venido haciendo, agrupamos los
términos mínimos. Una forma ideal de agruparlos sería:
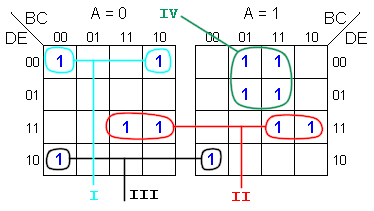
Vemos
que ningún término queda solo y que se hicieron la
menor cantidad de grupos posibles. Esta función quedaría
en su forma simplificada:
F=A'C'D'E'+BDE+B'C'DE'+ACD'
que son los
grupos I, II, III y IV respectivamente.
Por último,
para el caso de 6 variables tenemos 64 combinaciones posibles y la
forma para expresar el mapa que nosotros usaremos será:
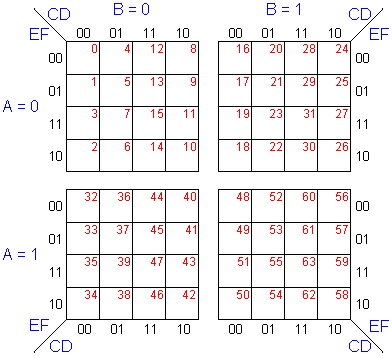
Se
observa que se separan los casos para A=0, A=1, B=0 y B=1. Por
supuesto que, como en el resto de los casos, todos los números
en las celdas hacen referencia a los términos mínimos.
También se cumple que los términos mínimos que
corresponden a cada celda pueden calcularse convirtiendo el número
binario de la respectiva combinación ABCDEF. Por ejemplo, para
ABCDEF=(101101)2=45, el término mínimo en la
celda es el m45. Aquí la adyacencia es un
poco más difícil de ver. Por ejemplo, las casillas con
los términos mínimos (63,62) es adyacente, además
de a todas las adyacencias normales del cuadro, a (47,46) y a
(31,30). Otro ejemplo, m0 es adyacente a m1,
m4, m2, m8, m16
y m32. (OJO: pero NO a m48 ya que
aquí hay dos variables distintas con respecto a m0).
Como
ejercicio, resuelva el siguiente mapa:
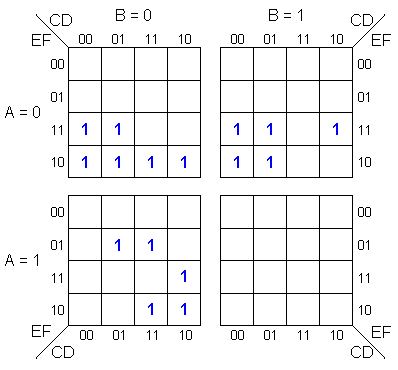
La
solución a este problema está en esta misma carpeta y
el nombre de la imagen solución es el mismo que el de la
imagen problema agregándole “_Solucion” (sin los
paréntesis) al final.
Para practicar les
voy a dar un programa “freeware” muy intuitivo y fácil
de usar, aunque limitado a 4 variables. Llenan la tabla de la verdad
y a medida que van colocando los unos, se va llenando el mapa de
Karnaugh, a la vez que se van agrupando los términos y
mostrando el resultado abajo. A/B/CD representa AB'C'D. Usan /X para
simular la raya sobre la letra que representa el símbolo de
negado (al igual que el tilde). También
se pueden marcar los unos directamente en el mapa de Karnaugh. Es un
archivo pequeño y no se requiere instalación. Hagan
click aquí para bajarlo.
#######################################################
NOTA AGREGADA: He
conseguido otro programa bastante bueno y gratuito. El programa fue
creado por Javier García Zubía y
su página web está en
http://paginaspersonales.deusto.es/zubia/.
Allí encontrarán varios links. El programa en cuestión
está en BOOLE-DEUSTO:
Descarga gratuita (español) . También
allí encuentran un manual en BOOLE-DEUSTO:
Manual (español). El programa que me
interesó más está dentro del archivo comprimido
BOOLE_SP con nombre boole.exe.
Si no quieren leer el
manual (cosa que deberían), luego de usarlo un rato se
entiende como funciona. No es para nada tan fácil de usar como
el otro programa que les di, pero si muchísimo más
completo con muchas más opciones. Muy Interesante. He hecho
ejemplos de hasta 12 variables. También tiene varios métodos
para la entrada de los datos. Pruébenlo.
#######################################################
Hagan el siguiente
ejercicio a mano y luego, con la tabla de la verdad o la forma
canónica que consiguieron, prueben el programa.
F(x, y, z,w) = x’y’z’w
+ x’y’z + x’yz’w' + xy’z’ + xyz’
Si lo
desea, puede ver otros puntos de vista de este tema en:
Para
la próxima clase veremos el tema
5: Condiciones irrelevantes (don't care). Universalidad de las
compuertas NAND y NOR.